publications
selected publications in reversed chronological order. Please refer to my Google Scholar profile for a full list.
2025
- ICML
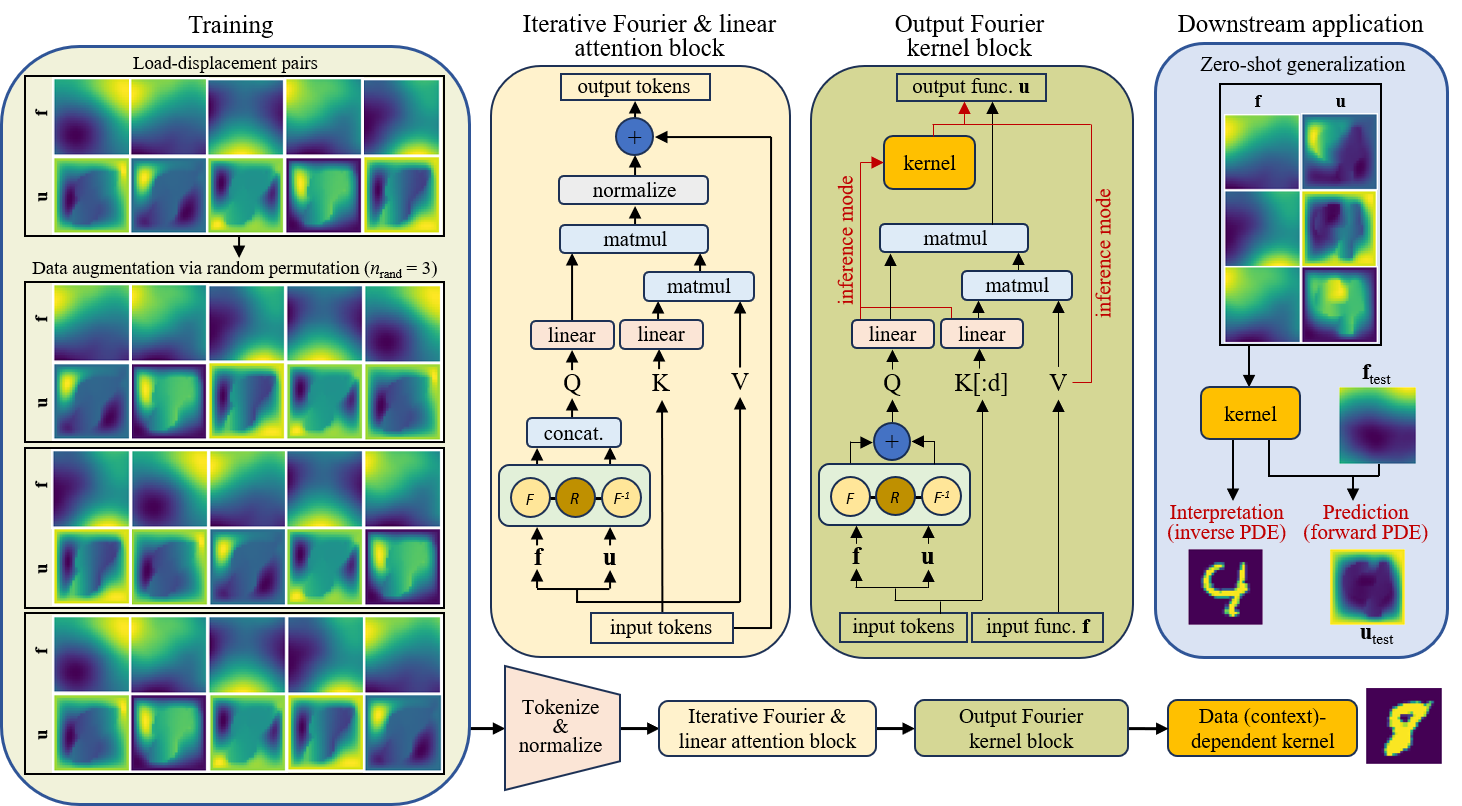 Neural Interpretable PDEs: Harmonizing Fourier Insights with Attention for Scalable and Interpretable Physics DiscoveryNing Liu, and Yue YuIn Forty-Second International Conference on Machine Learning, 2025
Neural Interpretable PDEs: Harmonizing Fourier Insights with Attention for Scalable and Interpretable Physics DiscoveryNing Liu, and Yue YuIn Forty-Second International Conference on Machine Learning, 2025Attention mechanisms have emerged as transformative tools in core AI domains such as natural language processing and computer vision. Yet, their largely untapped potential for modeling intricate physical systems presents a compelling frontier. Learning such systems often entails discovering operators that map between functional spaces using limited instances of function pairs – a task commonly framed as a severely ill-posed inverse PDE problem. In this work, we introduce Neural Interpretable PDEs (NIPS), a novel neural operator architecture that builds upon and enhances Nonlocal Attention Operators (NAO) in both predictive accuracy and computational efficiency. NIPS employs a linear attention mechanism to enable scalable learning and integrates a learnable kernel network that acts as a channel-independent convolution in Fourier space. As a consequence, NIPS eliminates the need to explicitly compute and store large pairwise interactions, effectively amortizing the cost of handling spatial interactions into the Fourier transform. Empirical evaluations demonstrate that NIPS consistently surpasses NAO and other baselines across diverse benchmarks, heralding a substantial leap in scalable, interpretable, and efficient physics learning.
- Nature Comput. Sci.
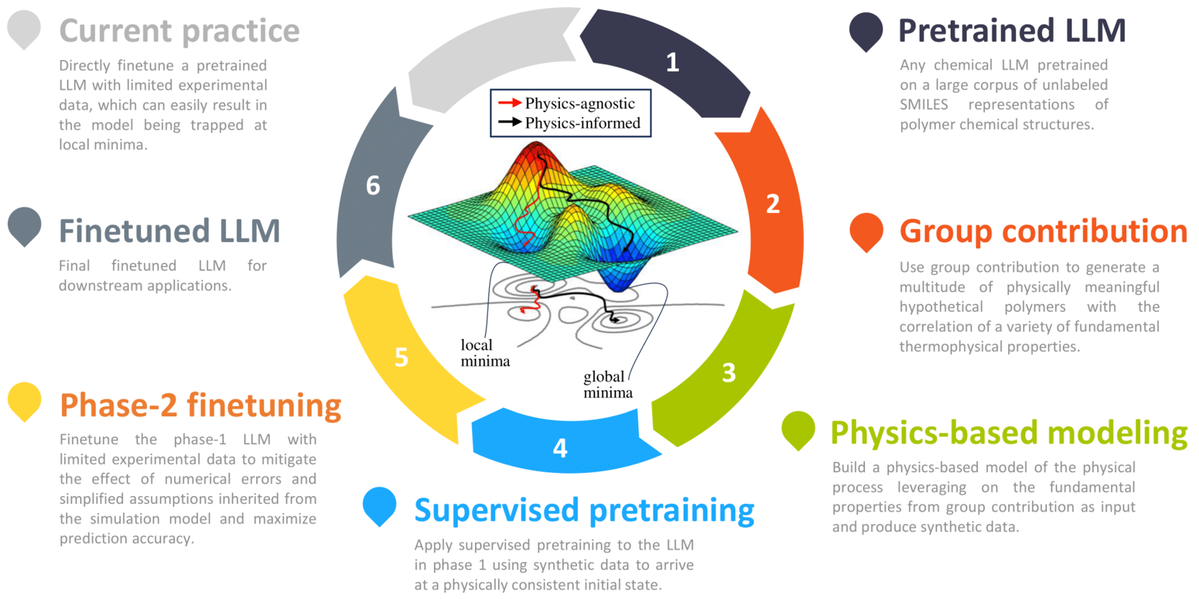 Harnessing large language models for data-scarce learning of polymer propertiesNing Liu, Siavash Jafarzadeh, Brian Y Lattimer, Shuna Ni, Jim Lua, and Yue YuNature Computational Science, 2025
Harnessing large language models for data-scarce learning of polymer propertiesNing Liu, Siavash Jafarzadeh, Brian Y Lattimer, Shuna Ni, Jim Lua, and Yue YuNature Computational Science, 2025Large language models (LLMs) bear promise as a fast and accurate material modeling paradigm for evaluation, analysis, and design. Their vast number of trainable parameters necessitates a wealth of data to achieve accuracy and mitigate overfitting. However, experimental measurements are often limited and costly to obtain in sufficient quantities for finetuning. To this end, we present a physics-based training pipeline that tackles the pathology of data scarcity. The core enabler is a physics-based modeling framework that generates a multitude of synthetic data to align the LLM to a physically consistent initial state before finetuning. Our framework features a two-phase training strategy: (1) utilizing the large-in-amount while less accurate synthetic data for supervised pretraining, and (2) finetuning the phase-1 model with limited experimental data. We empirically demonstrate that supervised pretraining is vital to obtaining accurate finetuned LLMs, via the lens of learning polymer flammability metrics where cone calorimeter data is sparse.
2024
- NeurIPS
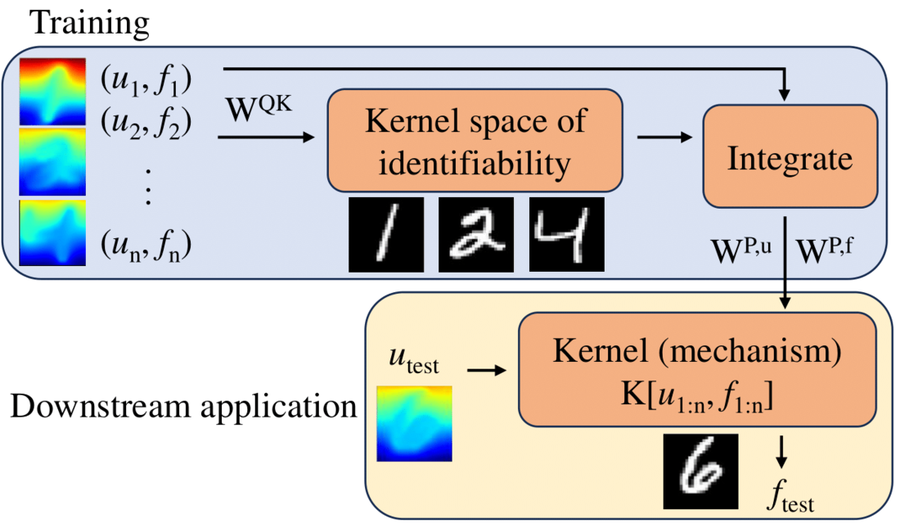 Nonlocal attention operator: Materializing hidden knowledge towards interpretable physics discoveryYue Yu, Ning Liu, Fei Lu, Tian Gao, Siavash Jafarzadeh, and Stewart SillingIn Thirty-Eighth Conference on Neural Information Processing Systems, 2024
Nonlocal attention operator: Materializing hidden knowledge towards interpretable physics discoveryYue Yu, Ning Liu, Fei Lu, Tian Gao, Siavash Jafarzadeh, and Stewart SillingIn Thirty-Eighth Conference on Neural Information Processing Systems, 2024Spotlight
Despite the recent popularity of attention-based neural architectures in core AI fields like natural language processing (NLP) and computer vision (CV), their potential in modeling complex physical systems remains under-explored. Learning problems in physical systems are often characterized as discovering operators that map between function spaces based on a few instances of function pairs. This task frequently presents a severely ill-posed PDE inverse problem. In this work, we propose a novel neural operator architecture based on the attention mechanism, which we coin Nonlocal Attention Operator (NAO), and explore its capability towards developing a foundation physical model. In particular, we show that the attention mechanism is equivalent to a double integral operator that enables nonlocal interactions among spatial tokens, with a data-dependent kernel characterizing the inverse mapping from data to the hidden parameter field of the underlying operator. As such, the attention mechanism extracts global prior information from training data generated by multiple systems, and suggests the exploratory space in the form of a nonlinear kernel map. Consequently, NAO can address ill-posedness and rank deficiency in inverse PDE problems by encoding regularization and achieving generalizability. We empirically demonstrate the advantages of NAO over baseline neural models in terms of generalizability to unseen data resolutions and system states. Our work not only suggests a novel neural operator architecture for learning interpretable foundation models of physical systems, but also offers a new perspective towards understanding the attention mechanism.
- ICML
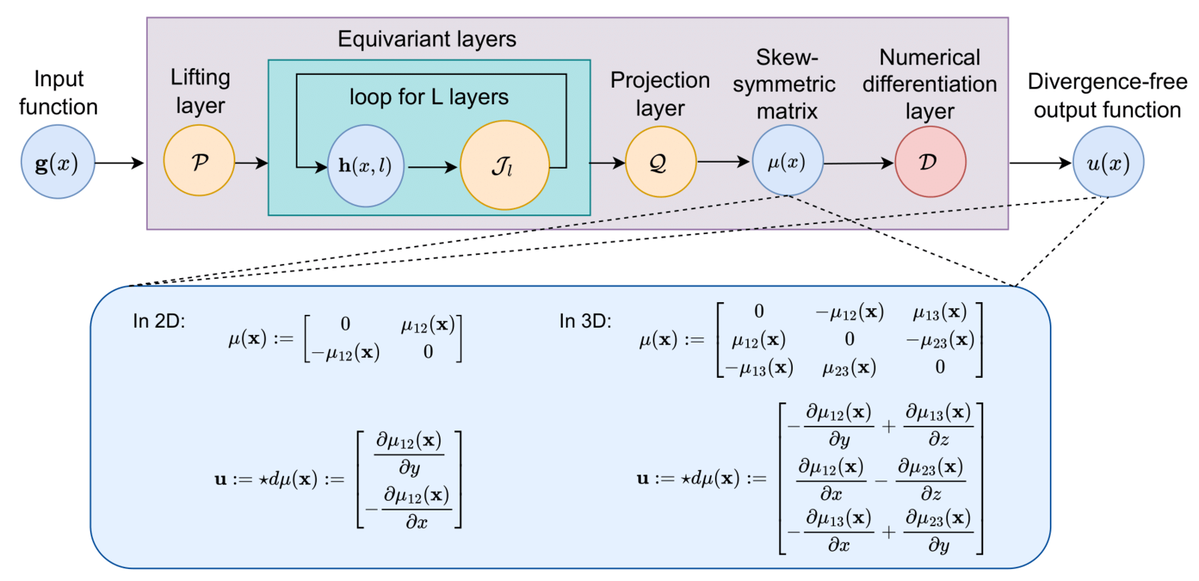 Harnessing the Power of Neural Operators with Automatically Encoded Conservation LawsNing Liu, Yiming Fan, Xianyi Zeng, Milan Klöwer, Lu Zhang, and Yue YuIn Forty-first International Conference on Machine Learning, 2024
Harnessing the Power of Neural Operators with Automatically Encoded Conservation LawsNing Liu, Yiming Fan, Xianyi Zeng, Milan Klöwer, Lu Zhang, and Yue YuIn Forty-first International Conference on Machine Learning, 2024Spotlight
Neural operators (NOs) have emerged as effective tools for modeling complex physical systems in scientific machine learning. In NOs, a central characteristic is to learn the governing physical laws directly from data. In contrast to other machine learning applications, partial knowledge is often known a priori about the physical system at hand whereby quantities such as mass, energy and momentum are exactly conserved. Currently, NOs have to learn these conservation laws from data and can only approximately satisfy them due to finite training data and random noise. In this work, we introduce conservation law-encoded neural operators (clawNOs), a suite of NOs that endow inference with automatic satisfaction of such conservation laws. ClawNOs are built with a divergence-free prediction of the solution field, with which the continuity equation is automatically guaranteed. As a consequence, clawNOs are compliant with the most fundamental and ubiquitous conservation laws essential for correct physical consistency. As demonstrations, we consider a wide variety of scientific applications ranging from constitutive modeling of material deformation, incompressible fluid dynamics, to atmospheric simulation. ClawNOs significantly outperform the state-of-the-art NOs in learning efficacy, especially in small-data regimes.
- CMAME
 Peridynamic neural operators: A data-driven nonlocal constitutive model for complex material responsesSiavash Jafarzadeh, Stewart Silling, Ning Liu, Zhongqiang Zhang, and Yue YuComputer Methods in Applied Mechanics and Engineering, 2024
Peridynamic neural operators: A data-driven nonlocal constitutive model for complex material responsesSiavash Jafarzadeh, Stewart Silling, Ning Liu, Zhongqiang Zhang, and Yue YuComputer Methods in Applied Mechanics and Engineering, 2024Neural operators, which can act as implicit solution operators of hidden governing equations, have recently become popular tools for learning the responses of complex real-world physical systems. Nevertheless, most neural operator applications have thus far been data-driven and neglect the intrinsic preservation of fundamental physical laws in data. In this work, we introduce a novel integral neural operator architecture called the Peridynamic Neural Operator (PNO) that learns a nonlocal constitutive law from data. This neural operator provides a forward model in the form of state-based peridynamics, with objectivity and momentum balance laws automatically guaranteed. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental data sets. We also compare the performances with baseline models that use predefined constitutive laws. We show that, owing to its ability to capture complex responses, our learned neural operator achieves improved accuracy and efficiency. Moreover, by preserving the essential physical laws within the neural network architecture, the PNO is robust in treating noisy data. The method shows generalizability to different domain configurations, external loadings, and discretizations.
- AIMS
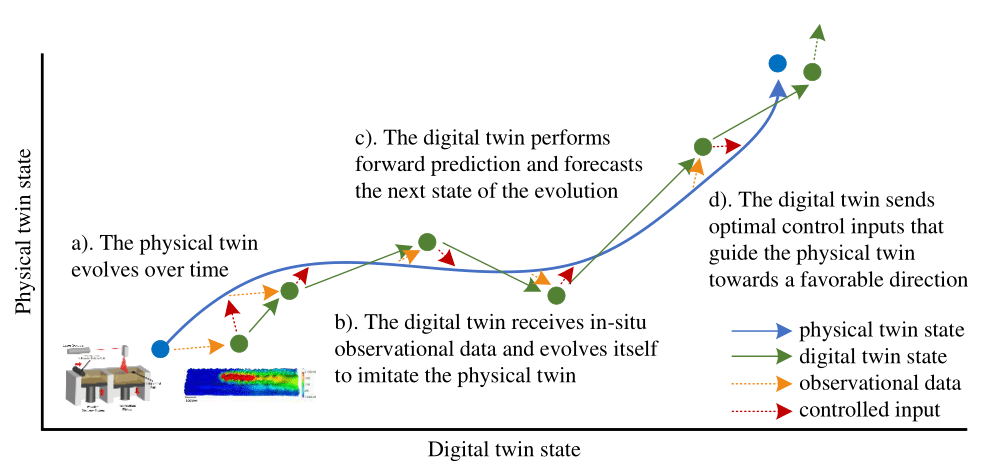 Deep Neural Operator Enabled Digital Twin Modeling for Additive ManufacturingNing Liu, Xuxiao Li, Manoj R Rajanna, Edward W Reutzel, Brady Sawyer, Prahalada Rao, Jim Lua, Nam Phan, and Yue YuAdvances in Computational Science and Engineering, 2024
Deep Neural Operator Enabled Digital Twin Modeling for Additive ManufacturingNing Liu, Xuxiao Li, Manoj R Rajanna, Edward W Reutzel, Brady Sawyer, Prahalada Rao, Jim Lua, Nam Phan, and Yue YuAdvances in Computational Science and Engineering, 2024A digital twin (DT), with the components of a physics-based model, a data-driven model, and a machine learning (ML) enabled efficient surrogate model, behaves as a virtual twin of the real-world physical process. In terms of Laser Powder Bed Fusion (L-PBF) based additive manufacturing (AM), a DT can predict the current and future states of the melt pool and the resulting defects corresponding to the input laser parameters, evolve itself by assimilating in-situ sensor data, and optimize the laser parameters to mitigate defect formation. In this paper, we present a deep neural operator enabled DT framework for closed-loop feedback control of the L-PBF process. This is accomplished by building a physics-based computational model to accurately represent the melt pool states, an efficient Fourier neural operator (FNO) based surrogate model to approximate the melt pool solution field, followed by a physics-based procedure to extract information from the computed melt pool simulation that can further be correlated to the defect quantities of interest (e.g., surface roughness). An optimization algorithm is then exercised to control laser input and minimize defects. On the other hand, the constructed DT also evolves with the physical twin via offline finetuning and online material calibration. For instance, the probabilistic distribution of laser absorptivity can be updated to match the real-time captured thermal image data. Finally, a probabilistic framework is adopted for uncertainty quantification. The developed DT is envisioned to guide the AM process and facilitate high-quality manufacturing in L-PBF-based metal AM.
2023
- NeurIPS
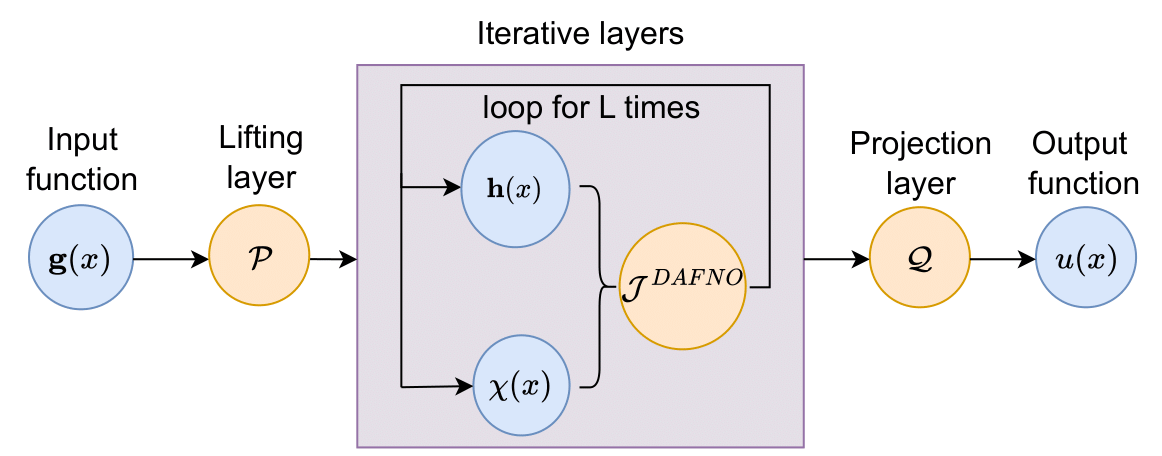 Domain agnostic fourier neural operatorsNing Liu, Siavash Jafarzadeh, and Yue YuIn Advances in Neural Information Processing Systems, 2023
Domain agnostic fourier neural operatorsNing Liu, Siavash Jafarzadeh, and Yue YuIn Advances in Neural Information Processing Systems, 2023Fourier neural operators (FNOs) can learn highly nonlinear mappings between function spaces, and have recently become a popular tool for learning responses of complex physical systems. However, to achieve good accuracy and efficiency, FNOs rely on the Fast Fourier transform (FFT), which is restricted to modeling problems on rectangular domains. To lift such a restriction and permit FFT on irregular geometries as well as topology changes, we introduce domain agnostic Fourier neural operator (DAFNO), a novel neural operator architecture for learning surrogates with irregular geometries and evolving domains. The key idea is to incorporate a smoothed characteristic function in the integral layer architecture of FNOs, and leverage FFT to achieve rapid computations, in such a way that the geometric information is explicitly encoded in the architecture. In our empirical evaluation, DAFNO has achieved state-of-the-art accuracy as compared to baseline neural operator models on two benchmark datasets of material modeling and airfoil simulation. To further demonstrate the capability and generalizability of DAFNO in handling complex domains with topology changes, we consider a brittle material fracture evolution problem. With only one training crack simulation sample, DAFNO has achieved generalizability to unseen loading scenarios and substantially different crack patterns from the trained scenario. Our code and data accompanying this paper are available at https://github.com/ningliu-iga/DAFNO.
- AISTATS
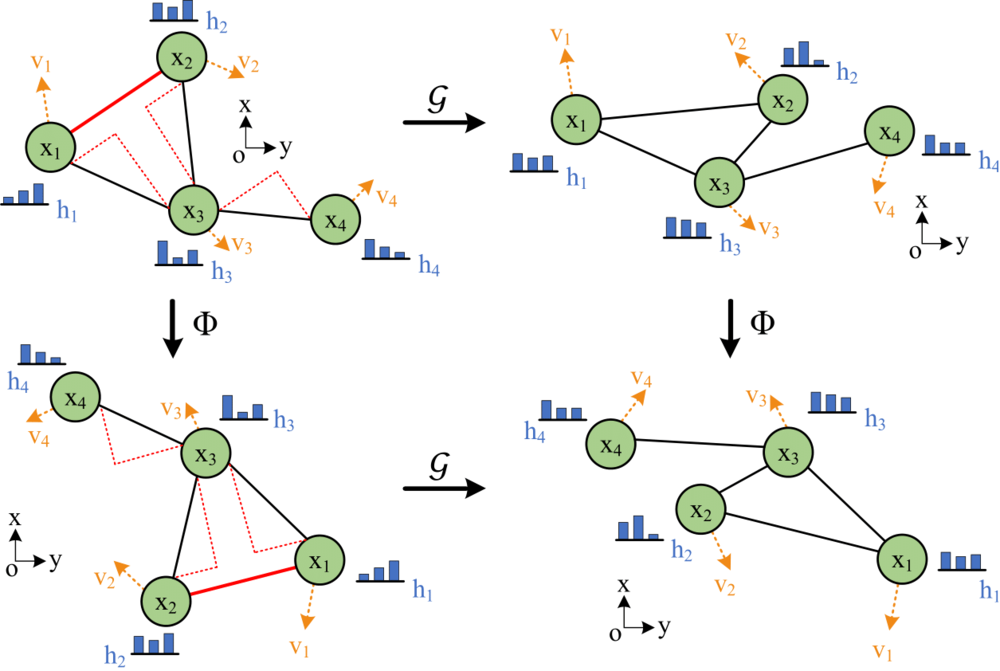 INO: Invariant neural operators for learning complex physical systems with momentum conservationNing Liu, Yue Yu, Huaiqian You, and Neeraj TatikolaIn International Conference on Artificial Intelligence and Statistics, 2023
INO: Invariant neural operators for learning complex physical systems with momentum conservationNing Liu, Yue Yu, Huaiqian You, and Neeraj TatikolaIn International Conference on Artificial Intelligence and Statistics, 2023Neural operators, which emerge as implicit solution operators of hidden governing equations, have recently become popular tools for learning responses of complex real-world physical systems. Nevertheless, the majority of neural operator applications has thus far been data-driven, which neglects the intrinsic preservation of fundamental physical laws in data. In this paper, we introduce a novel integral neural operator architecture, to learn physical models with fundamental conservation laws automatically guaranteed. In particular, by replacing the frame-dependent position information with its invariant counterpart in the kernel space, the proposed neural operator is designed to be translation- and rotation-invariant, and consequently abides by the conservation laws of linear and angular momentums. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental datasets, and show that, by automatically satisfying these essential physical laws, our learned neural operator is not only generalizable in handling translated and rotated datasets, but also achieves improved accuracy and efficiency from the baseline neural operator models.